Machine learning aims at replacing hand-coded functions with models automatically trained from data. Such automation is a reasonable and certainly inevitatable trend in computer science.
The main ‘trick’ however remains in training models that generalize well to unseen data. Training a model involves a potentially large set of data dubbed the training set. It is somewhat easy for the machine, and especially for deep neural networks to fully memorize these samples. The issue becomes that too much memorization leads to overfitting, which is the inability to generalize to novel, or at least previously unseen data.
Many real-world situations do arise where generalization is notoriously difficult:
- In low data regime typically.
- In large data regimes of synthethic data. In this case the training set may comes from simulations of the real-world that lack some tiny but nevertheless essential details. The discrepancy between the two data worlds often leads to a lack of generalization.
These situations can be mitigated with several tweaks, from [heavy data augmentation]() to [domain randomization and adaptation]().
Another way to improve generalization is to improve the training scheme itself, that looks for the best model parameters for the task. The training process navigates a very rugged multi-dimensional landscape of potential solutions. Along its search it can find a plethora of equivalently good solutions. Many of them however may be very tiny local minima.

The relationship between the shape of the solution landscape and model generalization has been studied extensively and remains somewhat elusive. Among uncovered useful directions, the flatness of the landscape surrounding a minimum apears to be correlated with better, more robust and generalized models.
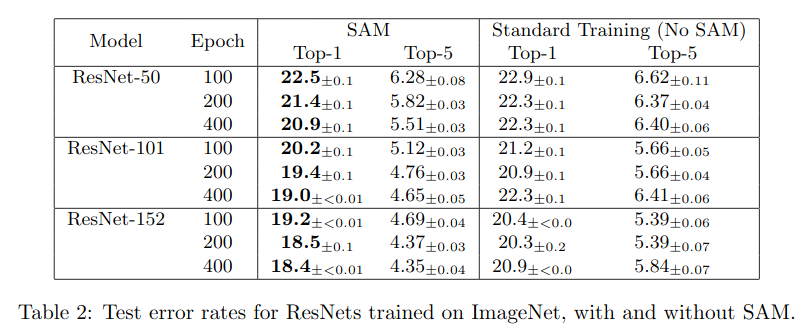
In their recent paper Sharpness-Aware Minimization for Efficiently Improving Generalization, Pierre Foret and others invent and investigate a novel optimization scheme for training deep model. The SAM optimization procedure combines both search for the best parameters with that of the flatness of the landscape that surrounds it.

The authors experiments show that SAM yields relevant improvements wrt. to accuracy, generalization and robustness. One drawbacks is its computational cost as a single optimization step now costs twice a regular parameter optimization step.
At Jolibrain we are convinced optimization is one of the key to better generalization and model training in general.
Thus a C++ version SAM has been recently added to DeepDetect’s collection of optimization methods. Our goal is to use it in our professional applications and report on advantages and drawbacks.
Our preliminary results indicate that SAM is competitive with other optimizers, and possibly better.
Using the DeepDetect API, simply set "sam":true within the JSON "solver" object. This activates the new optimizer as an option to any of the existing optimization techniques.
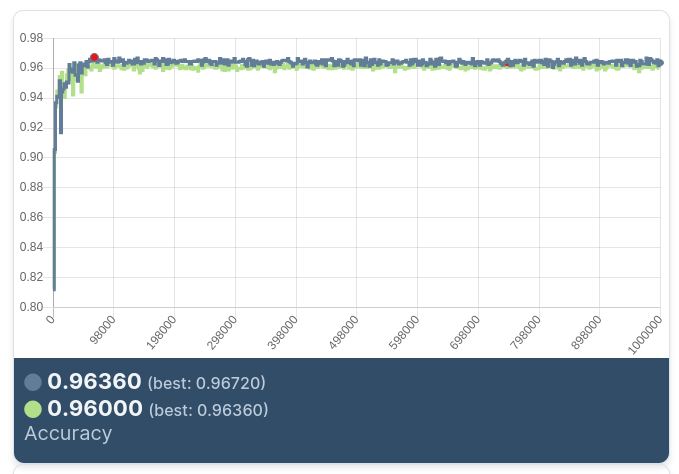
On a simple cats/dogs image classification problem (using the RANGER_PLUS DeepDetect optimizer), we get :
| nosam | sam | |
|---|---|---|
| best F1 | 0.963599 | 0.967186 |
| best iteration | 750 000 | 70 0000 |
which it seems to indicate that SAM behavres interestingly well. Not incredibly better, but better (especially on the time to best model).
Below is SAM testing curve in blue, slightly better: